Cara Menghitung Pembagian: Panduan Lengkap untuk Pemula

1. Pengertian Pembagian dalam Matematika

Pembagian adalah operasi aritmetika dasar yang merupakan kebalikan dari perkalian. Operasi ini digunakan untuk menghitung hasil bagi suatu bilangan terhadap pembaginya. Simbol pembagian yang umum digunakan adalah "÷", ":", atau garis miring (/).

Dalam operasi pembagian, terdapat tiga komponen utama yang perlu dipahami. Komponen pertama adalah dividen, yaitu angka yang akan dibagi. Komponen kedua adalah divisor atau pembagi, yaitu angka yang digunakan untuk membagi. Komponen ketiga adalah quotient atau hasil pembagian, yaitu hasil akhir dari operasi pembagian tersebut.

Rumus dasar pembagian dapat dituliskan sebagai: a ÷ b = c, di mana a adalah dividen, b adalah divisor, dan c adalah quotient. Sebagai contoh, dalam operasi 12 ÷ 3 = 4, angka 12 adalah dividen, 3 adalah divisor, dan 4 adalah hasil pembagian. Hubungan antara pembagian dan perkalian dapat dilihat dari rumus c × b = a.

Pembagian memiliki sifat-sifat khusus yang perlu diperhatikan. Pembagi tidak boleh bernilai nol (b ≠ 0) karena pembagian dengan nol tidak terdefinisi dalam matematika. Selain itu, pembagian tidak bersifat komutatif, artinya a ÷ b tidak sama dengan b ÷ a, berbeda dengan operasi perkalian atau penjumlahan.

2. Cara Menghitung Pembagian Dasar

Cara menghitung pembagian dasar dimulai dengan memahami tabel pembagian 1 hingga 10. Menghafal tabel pembagian ini akan sangat membantu dalam melakukan perhitungan yang lebih kompleks. Tabel pembagian merupakan kebalikan dari tabel perkalian yang sudah dipelajari sebelumnya.

Untuk pembagian bilangan kecil, Anda dapat menggunakan konsep perkalian terbalik. Misalnya, untuk menghitung 20 ÷ 4, Anda perlu mencari bilangan yang jika dikalikan 4 akan menghasilkan 20. Karena 4 × 5 = 20, maka 20 ÷ 4 = 5. Metode ini efektif untuk pembagian bilangan yang masih dalam jangkauan tabel perkalian dasar.

Pembagian juga dapat menghasilkan sisa. Ketika suatu bilangan tidak habis dibagi, akan ada sisa pembagian. Contohnya, 17 ÷ 5 = 3 sisa 2, karena 5 × 3 = 15, dan 17 - 15 = 2. Sisa pembagian selalu harus lebih kecil dari pembagi. Konsep pembagian dengan sisa ini penting dalam pembagian euclidean.

Untuk mempermudah perhitungan, ada beberapa aturan pembagian yang berguna. Bilangan habis dibagi 2 jika angka terakhirnya genap (0, 2, 4, 6, 8). Bilangan habis dibagi 5 jika angka terakhirnya 0 atau 5. Bilangan habis dibagi 10 jika angka terakhirnya 0. Aturan-aturan ini membantu mempercepat proses penghitungan pembagian.

3. Metode Pembagian Bersusun (Porogapit)

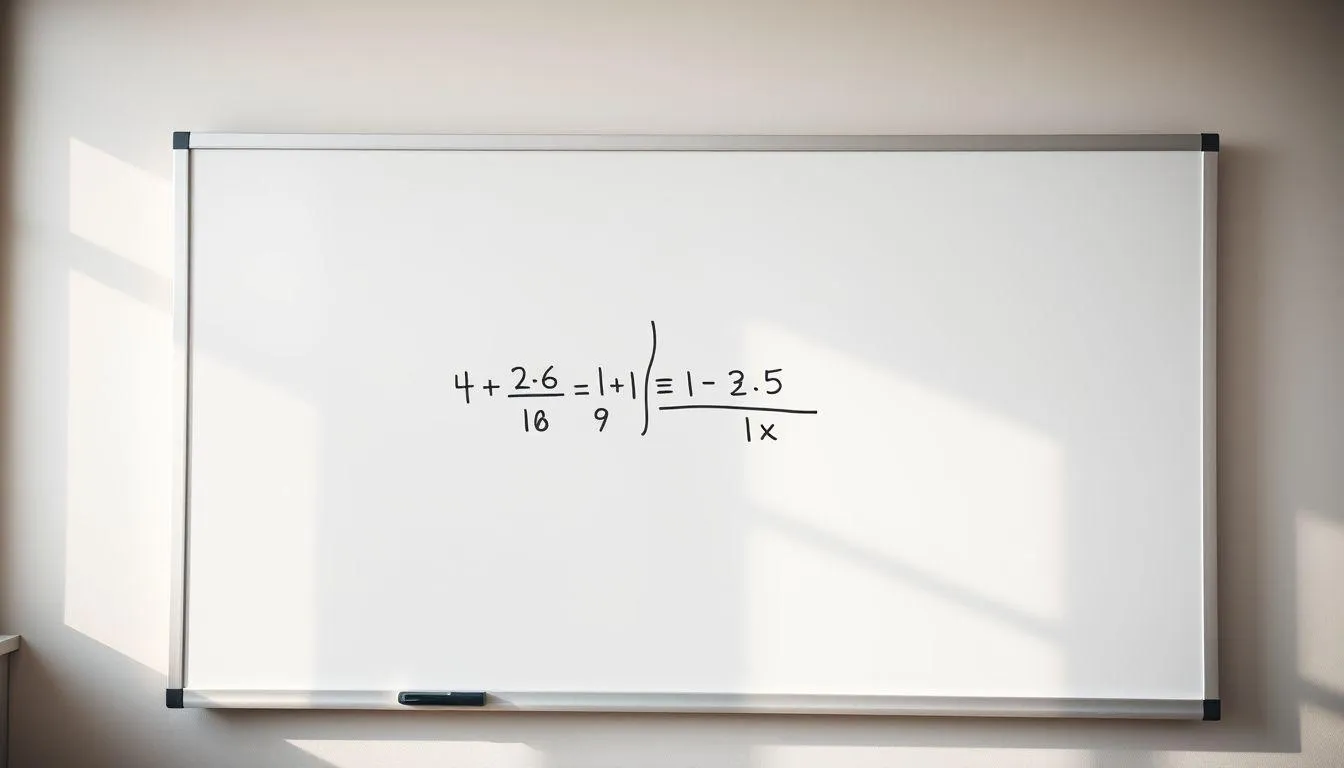
Pembagian bersusun atau porogapit adalah metode untuk menyelesaikan pembagian bilangan besar dengan menggunakan garis bantu. Metode ini sangat efektif untuk membagi bilangan yang terdiri dari dua angka atau lebih. Nama porogapit berasal dari bahasa Jawa, yaitu "poro" yang berarti bagi dan "gapit" yang berarti pengapit.

Langkah pertama dalam pembagian bersusun adalah membuat simbol pembagian dengan garis pengapit. Tuliskan bilangan yang dibagi (dividen) di dalam garis pengapit, dan bilangan pembagi (divisor) di sebelah kiri garis. Hasil pembagian akan dituliskan di atas garis pengapit. Pastikan penulisan angka sejajar dan rapi agar tidak terjadi kesalahan perhitungan.

Proses pembagian dimulai dari angka paling kiri (nilai tempat terbesar). Ambil angka pertama atau dua angka pertama dari dividen, tergantung apakah angka tersebut lebih besar dari divisor. Tentukan berapa kali divisor dapat dikalikan untuk mendekati angka tersebut tanpa melebihinya. Tuliskan hasil perkalian di bawah angka yang dibagi, lalu lakukan pengurangan.

Setelah pengurangan, turunkan angka berikutnya dari dividen dan gabungkan dengan sisa hasil pengurangan. Ulangi proses pembagian, perkalian, dan pengurangan hingga semua angka dari dividen telah diproses. Jika masih ada sisa setelah angka terakhir, itu menjadi sisa pembagian. Metode ini memungkinkan pembagian bilangan ratusan atau ribuan dilakukan secara sistematis dan terorganisir.

4. Langkah-Langkah Pembagian Bersusun Pendek

Pembagian bersusun pendek adalah variasi dari metode porogapit yang lebih efisien karena sebagian besar proses pengurangan dilakukan di dalam kepala. Metode ini menghemat waktu dan ruang di kertas, sehingga hasil pekerjaan terlihat lebih bersih dan rapi. Pembagian bersusun pendek cocok digunakan ketika pembagi adalah bilangan satu digit.

1. Siapkan Persamaan: Tuliskan bilangan yang dibagi di dalam simbol pembagian dan pembagi di sebelah kiri. Pastikan posisi angka sejajar dengan benar.
2. Bagi Angka Pertama: Mulai dari angka paling kiri, tentukan berapa kali pembagi dapat masuk ke dalam angka tersebut. Tuliskan hasilnya di atas garis pembagian.
3. Hitung Sisa Secara Mental: Kalikan hasil bagi dengan pembagi, lalu kurangkan dari angka yang dibagi. Jika ada sisa, tuliskan dalam ukuran kecil di depan angka berikutnya.
4. Gabungkan dengan Angka Berikutnya: Sisa dari pembagian sebelumnya digabungkan dengan angka berikutnya membentuk bilangan baru yang akan dibagi.
5. Ulangi Proses: Lakukan pembagian, perkalian mental, dan penulisan sisa untuk setiap angka hingga selesai. Pastikan tidak ada angka yang terlewat.
6. Periksa Hasil: Setelah selesai, verifikasi jawaban dengan mengalikan hasil bagi dengan pembagi, lalu tambahkan sisa jika ada. Hasilnya harus sama dengan bilangan yang dibagi.

Contoh penerapan: untuk menghitung 516 ÷ 4, mulai dengan 5 ÷ 4 = 1 sisa 1. Tuliskan sisa 1 kecil di depan angka 1, sehingga menjadi 11. Kemudian 11 ÷ 4 = 2 sisa 3. Tuliskan sisa 3 di depan angka 6, sehingga menjadi 36. Terakhir, 36 ÷ 4 = 9. Hasil akhirnya adalah 129.

5. Pembagian Bilangan Desimal

Pembagian desimal digunakan ketika hasil pembagian tidak menghasilkan bilangan bulat. Metode ini memberikan nilai yang lebih tepat dibandingkan hanya menuliskan sisa pembagian. Pembagian desimal sangat berguna dalam perhitungan yang memerlukan ketelitian tinggi, seperti dalam bidang sains dan keuangan.

Untuk melakukan pembagian desimal, lanjutkan proses pembagian bersusun hingga tidak ada angka lagi yang dapat diturunkan. Pada titik ini, tambahkan titik desimal pada hasil pembagian dan pada bilangan yang dibagi. Setelah titik desimal, setiap angka yang diturunkan adalah 0, sehingga bilangan yang dibagi menjadi, misalnya, 250.000.

Lanjutkan proses pembagian dengan menurunkan angka 0 setelah titik desimal. Bagi angka baru yang terbentuk dengan pembagi, lalu tuliskan hasilnya setelah titik desimal pada hasil pembagian. Ulangi proses ini hingga tidak ada sisa atau hingga mencapai tingkat ketelitian yang diinginkan. Dalam beberapa kasus, hasil desimal akan berulang terus-menerus.

Jika hasil desimal berulang, Anda perlu membulatkan jawaban. Bulatkan ke atas jika angka yang berulang adalah 5 atau lebih, dan bulatkan ke bawah jika angkanya 4 atau kurang. Sebagai contoh, dalam pembagian 250 ÷ 6, hasilnya adalah 41.666... yang dapat dibulatkan menjadi 41.67. Jangan lupa menambahkan satuan yang sesuai pada jawaban akhir.

6. Tips Menguasai Cara Menghitung Pembagian

Menguasai cara menghitung pembagian memerlukan latihan yang konsisten dan pemahaman konsep yang kuat. Langkah pertama adalah menghafal tabel perkalian 1 hingga 10 dengan sempurna, karena pembagian adalah kebalikan dari perkalian. Dengan menguasai tabel perkalian, Anda dapat dengan cepat menentukan hasil pembagian tanpa harus menghitung berulang kali.

Latihan rutin sangat penting untuk meningkatkan kecepatan dan akurasi. Mulailah dengan soal-soal pembagian sederhana, kemudian tingkatkan kesulitannya secara bertahap. Kerjakan berbagai jenis soal pembagian, termasuk pembagian dengan sisa, pembagian desimal, dan pembagian bilangan besar. Semakin banyak variasi soal yang dikerjakan, semakin terampil Anda dalam menghitung pembagian.

Gunakan teknik estimasi untuk memeriksa kewajaran jawaban. Sebelum menghitung secara detail, buatlah perkiraan kasar hasil pembagian. Misalnya, untuk 516 ÷ 4, Anda tahu bahwa 400 ÷ 4 = 100, jadi hasilnya pasti sedikit di atas 100. Teknik ini membantu mendeteksi kesalahan besar dalam perhitungan, seperti salah menempatkan titik desimal atau melupakan angka nol.

Pahami hubungan antara pembagian dan operasi matematika lainnya. Pembagian terkait erat dengan perkalian, pengurangan, dan pecahan. Memahami hubungan ini akan memperdalam pemahaman konseptual Anda. Selain itu, pelajari sifat-sifat pembagian, seperti pembagian dengan 1 menghasilkan bilangan itu sendiri, dan pembagian bilangan dengan dirinya sendiri menghasilkan 1. Pemahaman konseptual yang kuat akan membuat proses belajar lebih mudah dan menyenangkan.

7. FAQ (Pertanyaan yang Sering Diajukan)

Apa itu pembagian dalam matematika?

Pembagian adalah operasi aritmetika dasar yang merupakan kebalikan dari perkalian. Operasi ini digunakan untuk menghitung hasil bagi suatu bilangan terhadap pembaginya, dengan simbol "÷", ":", atau garis miring (/). Pembagian terdiri dari tiga komponen: dividen (bilangan yang dibagi), divisor (pembagi), dan quotient (hasil pembagian).

Bagaimana cara menghitung pembagian bersusun?

Pembagian bersusun atau porogapit dilakukan dengan membuat garis pengapit, menempatkan dividen di dalam dan divisor di luar. Mulai dari angka paling kiri, bagi dengan divisor, tuliskan hasilnya di atas, kalikan dan kurangkan, lalu turunkan angka berikutnya. Ulangi proses ini hingga semua angka selesai dibagi.

Apa perbedaan pembagian bersusun panjang dan pendek?

Pembagian bersusun panjang menuliskan setiap langkah perkalian dan pengurangan secara vertikal ke bawah, sehingga memerlukan lebih banyak ruang. Pembagian bersusun pendek melakukan sebagian besar pengurangan di dalam kepala dan hanya menuliskan sisa kecil di samping angka, sehingga lebih efisien dan rapi.

Bagaimana cara menghitung pembagian dengan sisa?

Pembagian dengan sisa terjadi ketika dividen tidak habis dibagi oleh divisor. Lakukan pembagian seperti biasa, dan angka yang tersisa setelah proses pembagian terakhir adalah sisa pembagian. Sisa pembagian harus selalu lebih kecil dari pembagi. Hasilnya dituliskan sebagai hasil bagi dan sisa, misalnya 17 ÷ 5 = 3 sisa 2.

Bagaimana cara membagi bilangan desimal?

Untuk membagi bilangan desimal, lanjutkan proses pembagian bersusun hingga tidak ada angka yang dapat diturunkan. Tambahkan titik desimal pada hasil dan dividen, lalu turunkan angka 0 setelah titik desimal. Lanjutkan pembagian hingga tidak ada sisa atau bulatkan hasil jika desimal berulang terus-menerus.

Mengapa pembagi tidak boleh nol?

Pembagian dengan nol tidak terdefinisi dalam matematika karena tidak ada bilangan yang jika dikalikan dengan nol akan menghasilkan bilangan selain nol. Jika kita mencoba membagi a ÷ 0 = c, maka seharusnya c × 0 = a, tetapi c × 0 selalu sama dengan 0, bukan a. Oleh karena itu, pembagian dengan nol tidak memiliki makna matematis.

Bagaimana cara cepat menguasai pembagian?

Cara cepat menguasai pembagian adalah dengan menghafal tabel perkalian 1-10, berlatih secara rutin dengan berbagai jenis soal, menggunakan teknik estimasi untuk memeriksa jawaban, dan memahami hubungan antara pembagian dengan operasi matematika lainnya. Konsistensi dalam berlatih adalah kunci utama untuk meningkatkan kecepatan dan akurasi dalam menghitung pembagian.